Ответ:
≈ 26 см
Объяснение:
Смотри рисунок в прикреплённом файле.
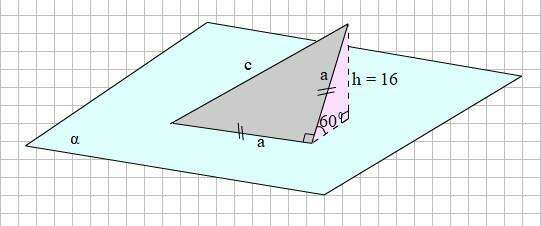
h = 16см - расстояние от вершины треугольника до плоскости α.
Катет а прямоугольного равнобедренного треугольника равен
а = h : sin 60° = 16 : 0,5√3 = 32/√3 (см)
Гипотенузу с прямоугольного равнобедренного треугольника со стороной а найдём по теореме Пифагора
с =√(а² + а²) = √(2а²) = а√2 = 32√2/√3 ≈ 26 (см)