Вычислить площадь фигуры ограниченной линиями у= -х^2+х+6, у= 2 - 2х

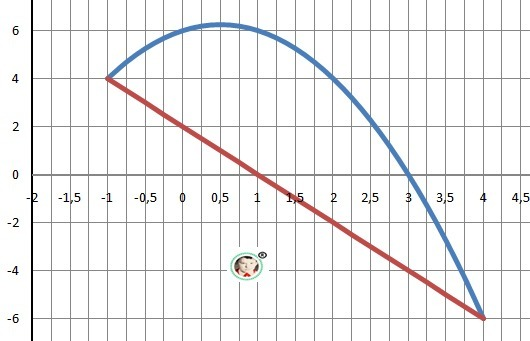
Дано: y1= - x²+x+6, y2 = - 2x + 2

Найти: S = ? - площадь.

Пошаговое объяснение:

Рисунок к задаче в приложении.

Площадь фигуры - разность интегралов функций.

Находим пределы интегрирования.

- x² + x+ 6 = 2 - 2x

x² - 3x - 4 = 0 - квадратное уравнение.

Пределы интегрирования: а = -1, b = 4.

Записываем разность функций (в обратном порядке для интегрирования).

$F(x)=\int\limits^4_b {(-4-3x+x^2)} \, dx=-\frac{4x}{1}-\frac{3x^2}{2}+\frac{x^3}{3}$

Вычисляем подставив пределы интегрирования.

F(4) = 4 - 1.5 - 1/3 = 2 1/6

F(-1) = -16 - 24 + 21 1/3

S = F(4)-F(1) = 20 5/6 - площадь - ответ.

Вычислить площадь фигуры ограниченной линиями у= -х^2+х+6, у= 2 - 2х ​