Пошаговое объяснение:
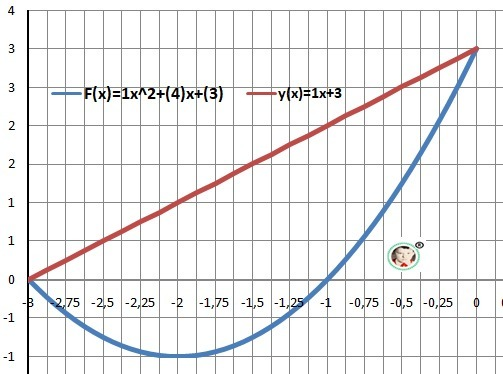
Дано: F(x)=x²+4x+3, y(x)=x+3
Найти: S=? - площадь фигуры
Решение:
1) Находим точки пересечения графиков.
-x²+-3*x+0=0 - квадратное уравнение
a = 0- верхний предел, b = -3- нижний предел.
2) Площадь - интеграл разности функций.
f(x) = -3*x -x^2 - подинтегральная функция
3) Интегрируем функцию и получаем:
F(x) = -3/2*x² -1/3*x³
4) Вычисляем значения на границах интегрирования.
S(a) = S(-3) = = 0+0+ 0 = 0
S(b) = S(0) =0+-13.5 + 9 = -4,5
S = S(a) - S(b) = 4,5 - площадь - ответ.
Рисунок к задаче в приложении.