Диагонали параллелограмма перпердикулярны и имеют длины 30 см и 16 см. найдите стороны...

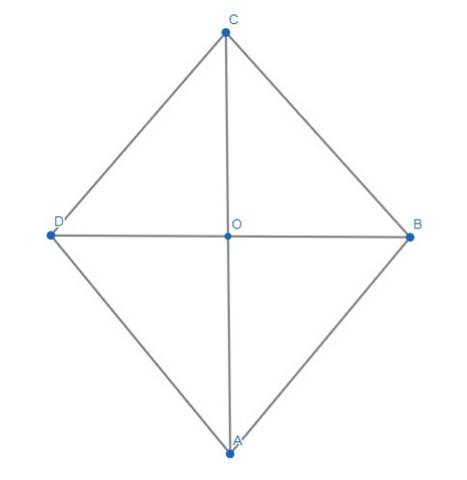
Отметим стороны параллелограмма буквами А В С и D (см. рисунок)

Дано: параллелограмм АВСD;

диагонали AC=30 cm, BD=16 cm;

AC⊥BD

Найти: АВ, СD, CB и AD

Решение: АС⊥BD (по усл.) ⇒ АВСD - ромб (1-ый признак ромба)

Пусть О - точка пересечения диагоналей АС и ВD.

Рассмотрим треугольник АОВ.

∡АОВ=90° (AC⊥BD) ⇒ АОВ прямоугольный.

АО = АС/2 = 30/2 = 15 cm

ОВ = ВD/2 = 16/2 = 8 cm

АВ= $\sqrt{OA^{2}+OB^{2}}$ = $\sqrt{8^2+15^2} }$ = $\sqrt{289}$ = 17 см (По т. Пифагора)

AB=CD=AD=CB=17 см

Ответ: стороны параллелограмма равны 17 см .