I. Последовательность действий
- Выделить массив от a[l] до a[r], где a - сортируемый массив, а l & r - крайний левый и крайний правый сортируемый елемент
- Провести сравнение елементов попарно двигаясь слева на право, если первый елемент больше второго - необходимо поменять их местами
- Откинуть крайнеправый елемент из сортируемого участка
- Провести сравнение елементов попарно двигаясь справа на лево, если первый елемент меньше второго - необходимо поменять их местами
- Откинуть крайне левый элемент из сортируемого участка
- Повторить с начала пока не останется сортируемых элементов
II. Оптимизация
Выполнение абсолютно всех проверок (прохождение по всем под массивам) не является обязательным при наличии механизма определяющего является ли массив отсортированным. Таковым может служить флаг, который будет выставлен при отсутствии перемещений элементов в выделенном под массиве на текущей итерации сортировки. Если он выставлен, следующая итерация - не выполняется.
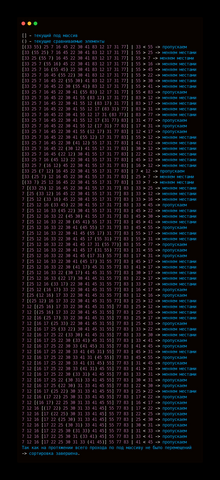
III. Пример сортировки
Элементы что находятся в текущем под массиве - выделены [] скобками.
Элементы что сравниваются в текущей итерации выделены ()
[(33 55) 25 7 16 45 22 30 41 83 12 17 31 77] | 33 < 55 -> пропускаем
[33 (55 25) 7 16 45 22 30 41 83 12 17 31 77] | 55 > 25 -> меняем местами
...
7 12 16 [17 22 25 30 31 (33 41) 45] 55 77 83 | 33 < 41 -> пропускаем
7 12 16 [17 22 25 30 31 33 (41 45)] 55 77 83 | 41 < 45 -> пропускаем
Так как на протяжении всего прохода по под массиву не было перемещений -> сортировка завершена.
(Полное решение представлено в прикрепленной картинке)
Кол-во сравнений при оптимизации сортировки: 71
Если считать кол-во сравнений в сортировке без оптимизации (либо в самом неудачном раскладе сорируемого массива) то его можно будет посчитать так:
кол-во сравнений 2n - 3 - для прохода по подмостиву туда и обратно (n - кол-во элементов массива)
кол-во сравнений в сортировке - сумма сравнений для прохода по каждому из под массивов туда и обратно
кол-во под массивов в массиве будет равно n / 2
Соответственно имеем формулу 
1}(2n-3)_{i};i=i-2" alt="\sum_{i=n}^{i>1}(2n-3)_{i};i=i-2" align="absmiddle" class="latex-formula">, или же другими словами: сумма элементов (2i - 3) от i, где i = n, пока i > 1, когда i = i - 2.
Ну и переведем её на наш пример:
n = 14
i = n
(2 * 14 - 3) + (2 * 12 - 3) + (2 * 10 - 3) + (2 * 8 - 3) + (2 * 6 - 3) + (2 * 4 - 3) + (2 * 2 - 3) =
25 + 21 + 17 + 13 + 9 + 5 + 1 = 91
Кол-во сравнений при оптимизации сортировки: 91
