Постройте график функции:у=(1-x^2)-(x^2-2)^2

Question

Дан 1 ответ

Правильный ответ

$y=(1-x^2)-(x^2-2)^2\\y=1-x^2-(x^4-4x^2+4)\\y=-x^4+3x^2-3\\x^2=a\\y=-a^2+3a-3;\\y=-(a^2-2*3a/2+(3/2)^2-(3/2)^2)-3\\y=-(a-3/2)^2+9/4-3\\y=-(x^2-3/2)^2-3/4\\y=-(x+\sqrt{\frac{3}{2}})^2(x-\sqrt{\frac{3}{2}})^2-0.75\\y'=-2(x+\sqrt{\frac{3}{2}})*(x-\sqrt{\frac{3}{2}})^2-2(x+\sqrt{\frac{3}{2}})^2*(x-\sqrt{\frac{3}{2}})$

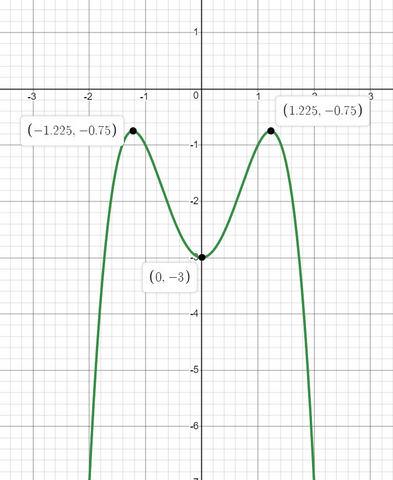
Найдём точки экстремумов.

$-2(x+\sqrt{\frac{3}{2}})*(x-\sqrt{\frac{3}{2}})^2-2(x+\sqrt{\frac{3}{2}})^2*(x-\sqrt{\frac{3}{2}})=0\\-2(x+\sqrt{\frac{3}{2}})(x-\sqrt{\frac{3}{2}})((x-\sqrt{\frac{3}{2}})+(x+\sqrt{\frac{3}{2}}))=0\\(x+\sqrt{\frac{3}{2}})(x-\sqrt{\frac{3}{2}})2x=0\\\left[\begin{array}{ccc}x=0\\x=-\sqrt{\frac{3}{2}}\\x=\sqrt{\frac{3}{2}}\end{array}$

Поймём где что, как.

\sqrt{\frac{3}{2}}\\-*+*+*+=-" alt="y'=-4x(x+\sqrt{\frac{3}{2}})(x-\sqrt{\frac{3}{2}})\\x>\sqrt{\frac{3}{2}}\\-*+*+*+=-" align="absmiddle" class="latex-formula">

Функция убывает.

$y'=-4x(x+\sqrt{\frac{3}{2}})(x-\sqrt{\frac{3}{2}})\\0<x<\sqrt{\frac{3}{2}}\\-*+*+*-=+$ Возрастает.

$y'=-4x(x+\sqrt{\frac{3}{2}})(x-\sqrt{\frac{3}{2}})\\-\sqrt{\frac{3}{2}}<x<0\\-*-*+*-=-$ Убывает.

$y'=-4x(x+\sqrt{\frac{3}{2}})(x-\sqrt{\frac{3}{2}})\\x<-\sqrt{\frac{3}{2}}\\-*-*-*-=+$ Возрастает.

$y=-(x+\sqrt{\frac{3}{2}})^2(x-\sqrt{\frac{3}{2}})^2-0.75$

Переменная, (+-) что-то в квадрате, значит функция будет расти и убывать достаточно быстро.

Найдём координаты точек экстремума по оси у.

$x=б\sqrt{\frac{3}{2}}\\y=-0.75$

Точки максимума: $(-\sqrt{\frac{3}{2}};-0.75)+and+(\sqrt{\frac{3}{2}};-0.75)$

Найдём координаты точки минимума.

$x=0\\y=-(0+\sqrt{\frac{3}{2}})^2(0-\sqrt{\frac{3}{2}})^2-0.75=\\-\frac{3*3}{2*2}-0.75=\\ -2.25-0.75=-3$

Есть координаты всех точке экстремумов, можем строить.

WhatYouNeed_zn (34.7k баллов) 29 Май, 20