В окружности радиуса 17 см проведена хорда . Найдите длину хорды , если она удалена от...

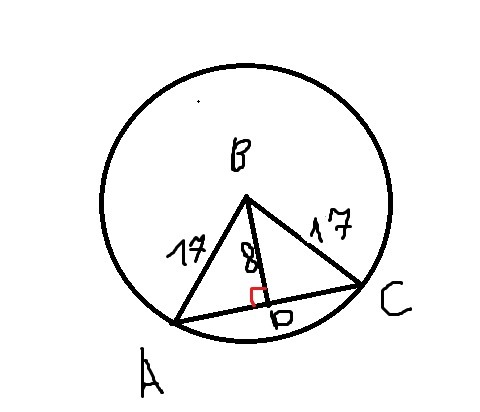
Дано:

Окружность с радиусом 17. Расстояние от хорды до центра окружности = 8

длину хорды

см. фото

перпендикуляр, опущенный из центра окружности на хорду делит её пополам.

Значит ABD - прямоугольный треугольник, при чём AD=DC

Найдём AD по т.Пифагора

AD= $\sqrt{17^{2}-8^{2}} =15$

Тогда вся хорда = AD*2=30