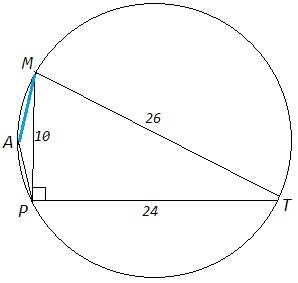
10^2 +24^2 =26^2
Для отрезков MP, PT, MT выполняется теорема Пифагора, следовательно треугольник MPT прямоугольный, MT - диаметр описанной окружности.
a) Сумма противоположных углов вписанного четырехугольника равна 180.
cos(MAP) = -cos(180-MAP) = -cos(MTP) = -PT/MT = -12/13
б) По теореме синусов
AM/sin(MPA) =2R <=> AM= 2R*sin(MPA) =26*6/13 =12
Но, MAP>90 (опирается на дугу больше 180) => MAP>MPA (в треугольнике может быть только один тупой угол), в треугольнике против большего угла лежит большая сторона, MP>AM, что противоречит найденному. Условие (б) некорректно.