Помогите пожалуйстаВычислить объем тела, образованного вращением вокруг оси ОХ фигуры,...

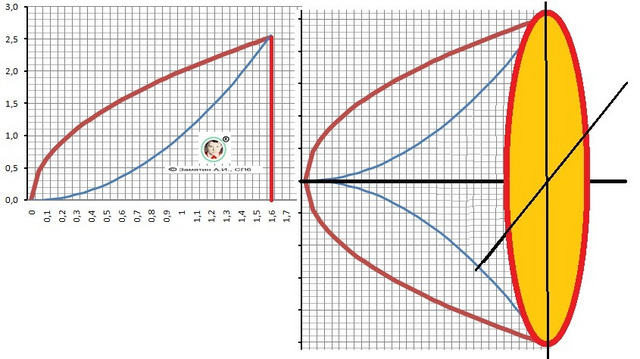
Дано: Y₁(x) = x², Y₂(x) = 2*√x.

Найти: V = ? - объём тела вращения.

Думаем: Формула вычисления объёма тела вращения вокруг оси ОХ: $V = \pi \int\limits^a_b {Y(x)^2} \, dx$

Пошаговое объяснение:

Рисунок с графиками функций и условное изображение фигуры - в приложении.

1. Находим пределы интегрирования - точки пересечения графиков.

2√x = x², 4x = x⁴, x³ = 4 x = ∛4 = a - верхний предел.

b = 0 - нижний предел. Вычисляем объём фигур по каждой функции, а затем найдём разность объёмов.

$V_{1}=\pi \int\limits{(\sqrt{x})^2 } \, dx=\pi \int\limits^a_b {x} \, dx=\pi \frac{x^2}{2}$

V = π*a/2 = 0.7937

$V_{2}=\pi \int\limits{(x^2)^2} \, dx=\pi \frac{x^5}{5}$

V₂ = a⁵/5

Формулы записали - остаётся вычислить разность разностей.

V1(b) = 0

V1(a) = π*a/2 = 1/2*π*∛4 - объем под графиком корня.

V2(b) = 0

$V_{2}(\sqrt[3]{4}) = \pi\frac{\sqrt[3]{4}^5}{5}=\pi\frac{\sqrt[3]{x^!0} }{5}}=\pi\frac{8}{5}\sqrt[3]{2}$ - объём под параболой.

V1 = 1.26*π и V2 = 2.016*π

И находим разность объёмов.

Что-то трудно и прочитать формулы и записать их. Возможны опечатки.