1.
Ответ: нет решений.
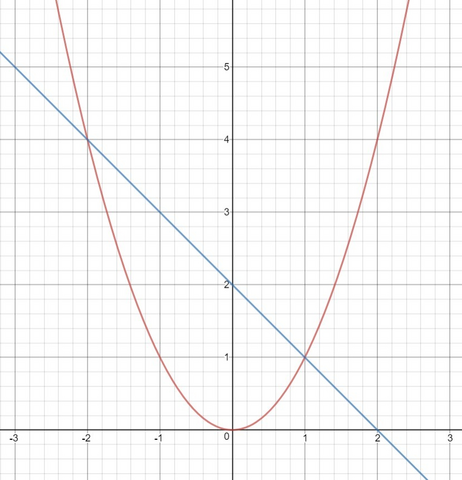
2. f1(x)=f2(x), найдём их точки пересечения. 
То есть координаты общих точек по оси х это -2 и 1.
Найдём по оси y. f2(-2)= -(-2)+2=4; f2(1)= -(1)+2=1
Ответ: (-2;4) и (1;1). так же см. график внизу.
3. a,b -стороны прямоугольника; S-площадь; P-периметр.
 a=\frac{26}{2} -b}} \right. \\" alt="\left \{ {{S=a*b=40} \atop {P=2(a+b)=26=>a=\frac{26}{2} -b}} \right. \\" align="absmiddle" class="latex-formula">
a=\frac{26}{2} -b}} \right. \\" alt="\left \{ {{S=a*b=40} \atop {P=2(a+b)=26=>a=\frac{26}{2} -b}} \right. \\" align="absmiddle" class="latex-formula">
Подставим это значение в первое уравнение.

Тогда 
Ответ: 5 и 8.