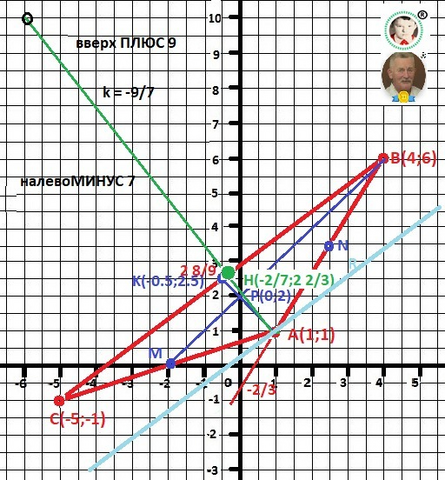
Рисунок в приложении.
Дано: А(1;1), В(4;5), С(-5;-1)
Решение треугольника.
А. Уравнения сторон.
Формулы: k = (By - Ay)/(Bx - Ax), b = Ay - k*Ax.
АВ = 5/3*x - 2/3 и AC = 1/3*x + 2/3 и BC = 7/9*x +2 8/9 - ответ
Б. Уравнения медиан.
1. Координаты середины стороны.
Ме(А) = К - середина стороны АВ.
Кх = (Ax+Bx)/2 = -0.5, Ky = (Ay+By)/2 = 2.5,
Me(A) = K(-0.5;2.5), Me(B) = M(-2;0), Me(C) =N(2.5;3.5).
2. Уравнения медиан.
АК = -x +2, BM = x +2 - ответ, CN = 3/5*x + 2.
3. Точка пересечения медиан АК и ВМ.
Решение системы уравнений:
1) x + y = 2
2) - x + y = 2
Сложили уравнения: 2*y = 4, y = 2, x = 0
Р(0;2) - точка пересечения медиан - ответ.
В. Уравнение высоты АН - перпендикулярно ВС и её длина.
1. Уравнение перпендикулярной прямой через т.А(1;1).
k(BC) = 7/9 - см. выше. k2 = k(AH) = - 1/k(BC) = - 9/7 = - 1 2/7 - наклон
b = Ay - k2*Ax = 2 2/7 - сдвиг.
y(AH) = - 1 2/7*x + 2 2/7 - уравнение высоты - ответ.
2. Координата точки Н - пересечение прямых АН и ВС. (см.выше).
Н(-2/7;2 2/3) - координата точки Н - решение.
3. Длина отрезка AH - между точками.
По теореме Пифагора.
L(AH) = √((Ay-Hy)² + (Ax-Hx)²) ,
L² = (1 2/3)² + (1 2/7)² = 2.778 + 1.653 = 4.431
L = √4.431 = 2.105 ≈ 2.1 - длина высоты АН - ответ.
Г. Уравнение прямой параллельной прямой ВС через т. А.
Коэффициент наклона - k = k(BC) = 7/9 - наклон
b= Ay - k*Ax = 1 - 7/9*1 = 2/9 - сдвиг.
Уравнение прямой R - y = 7/9*x + 2/9 - ответ.
Д. Внутренний угол В - между прямыми АВ и ВС.
По формуле: тангенс разности углов.

Коэффициенты наклона - k1 = k(АВ) = 1 2/3, k2 = 7/9
1) k2 - k1 = 8/9
2) 1 + k1*k2 = 2 8/27
3) tgα = 12/31 = 0.387
4) α = arctg(0.387) = 0.37 (рад) - угол В - ответ. (= 21° 9' 40")