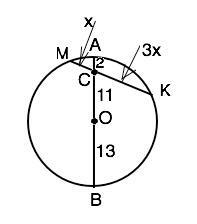
Обозначим диаметр ( наибольшую хорду окружности) АВ. Хорду, проходящую через точку С - МК. По свойству пересекающихся хорд при пересечении двух хорд окружности произведение отрезков одной хорды равно произведению отрезков другой хорды. ⇒ АС•СВ=МС•СК. Длина диаметра 2R=2•13=26 см. Точка С делит диаметр на отрезки ВС=R+OC=13+11=24 см и АС=26-24=2 см. Примем МС=х, а СК=3х. . 2•24=х•3х ⇒ 3х²=48 ⇒х²=16 ⇒ х=√16=4 см. Отсюда МК=х+3х=4х. ⇒ хорда МК=4•4=16 см