Дан треугольник ABC, BM- его медиана. Известно, что BM=1/2 AC. Угол A равен 65°. Найдите...

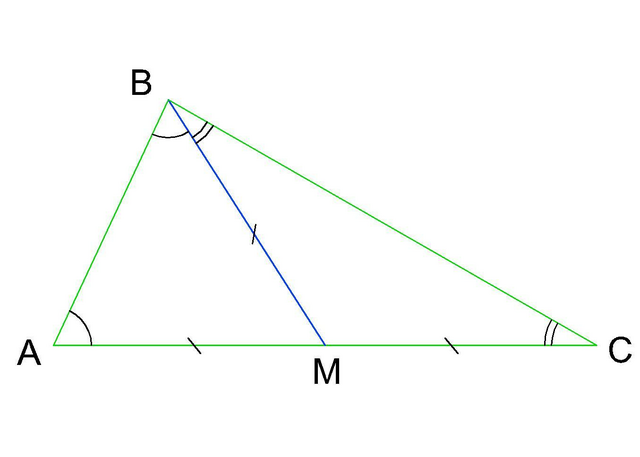
Т.к. ВМ медиана, то она делит сторону АС на МА=МС= $\frac{1}{2}$ АС. Если ВМ тоже равно $\frac{1}{2}$ АС, то ΔАМВ и ΔСМВ - равнобедренные.

В ΔАМВ ∠А=∠АВМ=65°, тогда ∠АМВ=180-2·∠А=180-130=50°.

В равнобедренном ΔСМВ ∠ВМС =180-∠АМВ=180-50=130°. Найдем остальные два равных угла при основании ΔСМВ.

∠С=∠СВМ=(180-∠ВМС)/2=(180-130)/2=25°

Ответ: ∠С=25°