1. То, что стороны многоугольника удалены от его центра на расстояние 
, означает, что радиус вписанной окружности равен . Значит отношение радиуса описаной к радиусу вписанной окружностей = 2.
Тогда используя формулы описанной окружности: R=a/(2sin (360°/2n))
и формулу вписанной окружности: r=a/(2tg (360°/2n)), где n-число сторон многоугольника, а- длина стороны многоугольника, получаем уравнение:
=2
=2
cos(360/2n)=1/2
360/2n=60
360=120n
n=3
Ответ: число сторон правильного многоугольника равно 3.
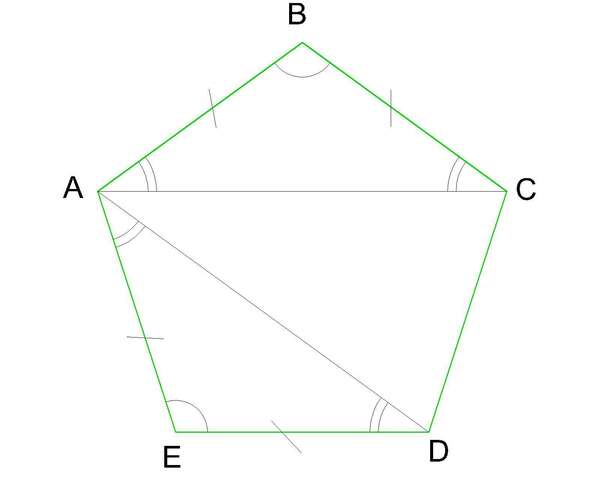
2. В правильном пятиугольнике все стороны равны и все внутренние углы равны.
Найдем внутренний угол пятиугольника: α=
·180°=
·180=108°
Значит внутренний ∠ВАЕ=108°.
Рассмотрим рисунок.
Диагонали АС и АД образуют 2 равных равнобедренных ΔАВС и ΔАЕД, где основаниями являются диагонали пятиугольника.
Докажем равенство треугольников: ∠АВС=∠АЕД=108°, АВ=ВС=АЕ=ЕД. Равенство доказано по 2-м сторонам и углу между ними.
Т.к. ΔАВС и ΔАЕД - равнобедренные, то уних углы при основаниях равны: ∠ВАС=∠ВСА=∠ДАЕ=∠ЕДА=(180-108)/2=36° (из суммы углов треугольника)
Рассмотрим ∠ВАЕ=108°=∠ВАС+∠ДАЕ+∠САД
∠САД=108-(∠ВАС+∠ДАЕ)=108-36-36=36°
∠ВАС=∠ДАЕ=∠САД=36°
Доказано: диагонали АС и АД делят ∠ВАЕ=108° на 3 равных части по 36°.
(Внимание, в решении этих задач, при употреблении слов "многоугольник" или "пятиугольник" всегда имелось ввиду, что он правильный, т.е. равносторонний)
