3) ** стороне AB треугольника ABC отмечена точка M так, что AM:MB=6:7. В каком отношении...

Question

3) На стороне AB треугольника ABC отмечена точка M так, что AM:MB=6:7. В каком отношении медиана BK делит отрезок CM? 4) Через точку P, которая лежит внутри окружности, проведена хорда, которая делится точкой P на отрезки, длины которых равны 4 и 5. Найдите расстояние от точки P до центра окружности, если радиус окружности равен 6 см.

Comments

к каждому заданию рисунок

Answer 1

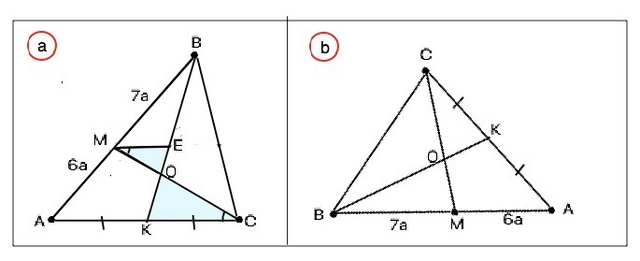
1.а) Проведем МЕ||АК. Треугольники  АВК ~ МВЕ по дву углам: угол при вершине В общий, угол ВМЕ=ВАК как соответственные при пересечении параллельных АЕ и АК секущей ВА.   Из отношения

АМ:ВМ сторона АВ=6+7=13 частей. ВМ:ВА=7/13 ⇒ МЕ:АК=7/13. Так как КС=АК, МЕ:КС=7/13. ∆ МОЕ~∆ КОС по двум углам ( углы при О - вертикальные, углы при М и С - накрестлежащие). ⇒ МО:ОС=МЕ:КС=7/13

Или

1.b) По т.Менелая: (АК:КС)•(СО:ОМ)•(ВМ:АВ)=1, откуда СО:ОМ=АК•ВМ:СК•АВ=1•7:1•13, т.е. СО:ОМ=13/7 и ОМ:СО=7/13

––––––––––––––

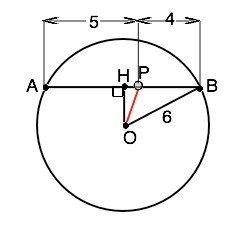
2. Если центр окружности О, искомое расстояние ОР. Обозначим хорду АВ. АВ=4+5=9 см. Проведём из центра окружности перпендикуляр ОН к хорде. По свойству радиуса он делит хорду  пополам. АН=НВ = АВ:2 ⇒  АН=9:2=4,5 см. РН=ВН-РВ=4,5-4=0,5 см. Из прямоугольного⊿ ОНВ по т.Пифагора ОН²=OB²-BH²=6²-4,5²= 15,75  Из ⊿ ОНР по т.Пифагора OP=√(OH²+PH²)=√16=4 (см)

---

---

Comments

спсибо