В правильной четырёхугольной пирамиде сторона основания равна 6 см, угол между боковым...

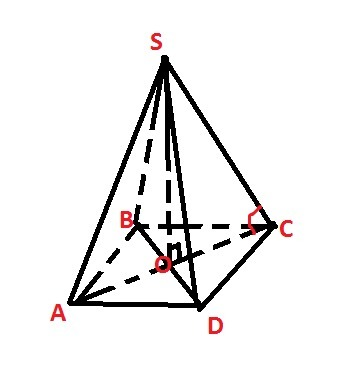
См. рис.

Для нахождения бокового ребра рассмотрим треугольник SOC, в котором нам известен угол, а прилежащий катет мы можем найти.

АС - диагональ квадрата АВСД, т. О делит АС пополам, следовательно, ОС равен половине диагонали квадрата. ОС=6√2:2=3√2.

В треугольнике SOC через косинус угла в 30 градусов находим боковое ребро SC. SC= $3\sqrt{2} *\frac{2}{\sqrt{3} } =\frac{6\sqrt{2} }{\sqrt{3} } =2\sqrt{6}$

В пирамиде проводим апофему SK (т. К - середина стороны ДС). из т. О опускаем перпендикуляр на ДС. Т.к. фигура правильная, перпендикуляр на ДС совпадет с точкой К, следовательно, получаем треугольник SОК, где искомый двугранный угол - угол SКО. Боковое ребро мы уже знаем, КС = 6:2=3. Из прямоугольного треугольника SКС находим апофему SК по т. Пиф. SК = корень из 15. Синус SКО равен корень из 6 делить на корень из 15, преобразуем и получим, что угол равен арксинус корень из 10 делить на 5.