Даю 100 баллов y=(x4–13x2+36)/((x–3)(x+2)) только когда график строить будете через...

Область определения функции: x≠3; x≠-2

Преобразуем:

$\sf y=\dfrac{x^4-13x^2+36}{(x-3)(x+2)}=\dfrac{(x^4-12x^2+36)-x^2}{x^2-x-6}=\dfrac{(x^2-6)^2-x^2}{x^2-x-6}= \\ \\=\dfrac{(x^2-x-6)(x^2+x-6)}{x^2-x-6}=x^2+x-6$

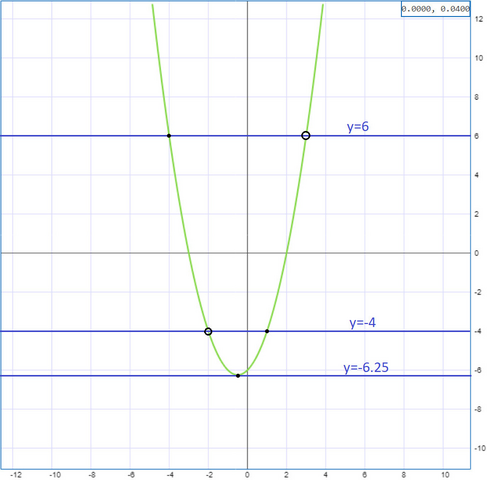
Точки для графика: (-4; 6), (-3; 0), (-2; -4) - выколота, (-1; -6), (0; -6), (1; -4), (2; 0), (3; 6) - выколота.

График функции представляет собой параболу с двумя выколотыми точками. Прямая y=c будет иметь с ним только одну общую точку, если она пройдет через одну из выколотых точек, откуда c₁=6, c₂=-4, либо через вершину параболы x₀=-0.5 ⇒ y₀=c₃=-6.25.

Ответ: c=6; c=-4; c=-6.25