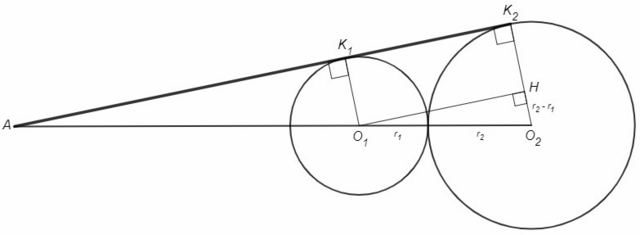
Две окружности с радиусами 4 см и 6 см касаются внешним образом. Их общая касательная, не проходящая через точку касания окружностей, пересекает линию центров в точке А. Найти расстояние от точки А до центров окружностей.
O1, O2 - центры окружностей, r1
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
O1H⊥O2K2, O1K1K2H - прямоугольник, HK2=r1
O2H=r2-r1
O1O2=r1+r2 (точка касания лежит на линии центров)
△O1O2H~△AO1K1~△AO2K2 (параллельные отсекают от угла подобные треугольники)
AO1= r1(r1+r2)/(r2-r1) =4*10/2 =20
AO2= r2(r1+r2)/(r2-r1) =6*10/2 =30