Y=-x³+ 1 [-2;0] Исследовать функцию построить её график найти наибольшее и наименьшее...

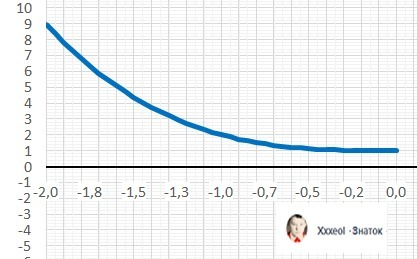
Дано: y = -x³ + 1

D(y) = [-2;0] - область определения.

Пошаговое объяснение:

1. Гладкая непрерывная функция - график в приложении.

2. Нуль функции: Y(x) = 0, x = 1.

3. На D(y) - убывает.

4. Максимум: Y(-2) = 9, минимум: Y(0) = 1.

5. Площади - интеграл функции. a = 0, b = - 2

$S=\int\limits^a_b {(1-x^3)} \, dx=\frac{x}{1}-\frac{x^4}{4}$

Именно такая запись мне нравится при интегрировании функций - степень увеличивается (в числителе), а знаменателе - значение этой степени.

6. Вычисляем на границах интегрирования

S(0) =0, S(-2) = -2 - 16/4 = - 6. S = 0 - (-6) = 6 - площадь - ответ.