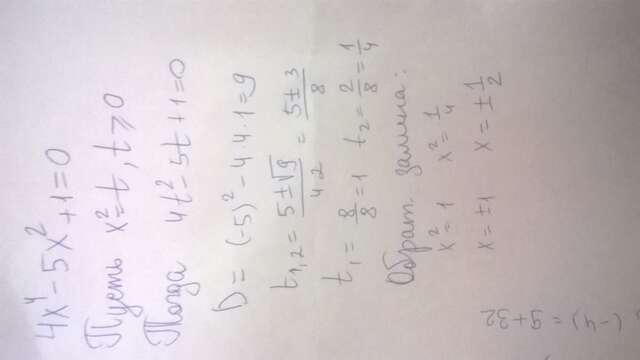Квадратные-вида ax^2+bx+c
a,b,c-коэффициенты перед переменными,решются квадратные уравнения различными способами:через дискриминант ,через теорему Виета,формулы дискриминанта:D=b^2-4ac,где a,b,c коэффициенты,представленные выше,если D>0-2 корня,если <0-корней нет, =0 -1 корень,дальше искать x1 и x2-корни нашего уравнения,находятся п формуле x1,2=-b+- корень из D/2a,x1=-b+корень из D/2a,x2=-b- корень из D/2a,не забывай,если коэффициент b уже с минусом,то в формуле оно станет положительным(2 минуса дают плюс)про Виета не стан особо говорить,дискриминанта часто бывает достаточно,ибо Виета понимают далеко не все,многим привычнее через D.Также бывают неполные квадратные, картинка внизу,можно решить вынесением общего множителя за скобку,полученные выражения приравнять к 0.примеры решений во вложении,биквадратное- уравнение четвертой степени,решается методом замены переменной(x^2=t(либо любая другая буква)),после идет обратная замена(подробнее во вложении)</p>