1. По первому признаку подобия треугольников будут подобны любые два .(?) треугольника.
I. Признак подобия треугольников по двум углам.
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Так как острые углы
равнобедренных прямоугольных треугольников равны 45º, то по этому признаку подобны:
5. любые два равнобедренных прямоугольных треугольника
.----------------
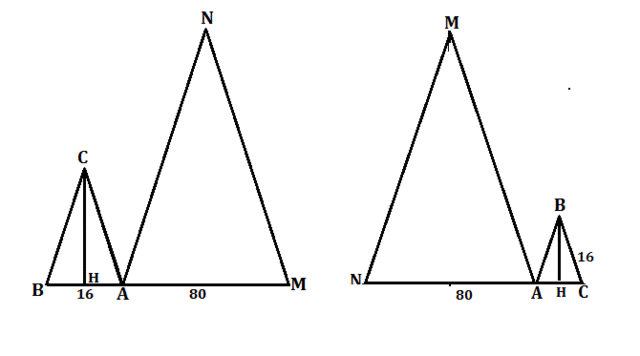
2.Треугольники АВС и AMN - равнобедренные. Периметр треугольника AMN равен 320 см, АВ=16 см, АМ=80 см. Найдите площадь треугольника АВС.
Задача не совсем корректна. Приходится по теме вопроса догадываться, что данные треугольники подобны.
В треугольнике АМN сторона АМ=80.
Из неравенства треугольников следует, что только АМ может быть основанием этого треугольника, и АN=МN=(320-80):2=120
Тогда
Вариант 1
)
АВ=16- основание меньшего треугольника
k=АМ:АВ=80
:16=5
ВС=АС=120
:5=24
Высоту СН ∆ АВС найдем по т.Пифагора
:
СН=√(ВС²-ВН²)=√512=16√2
Ѕ∆ АВС=ВН*СН=8*16√2=128√2 см² или ≈181,02 см²
Вариант 2)
АВ=16 - боковая сторона меньшего треугольника.
Тогда k=AM:BC=120:16=7,5
АС=80
:7,5=32/3
Тогда
СН=АС:2=
16/3
Высота ВН=√(BC² -CH²)=√(9*256-256):9)=√(8*256:9)=√(2*4*256:3)=(32√2)/3
S ∆АВС=ВН*СН=(32√2)/3)*16/3
S ∆АВС=(32*16√2)/9 см² или ≈ 80,453 см²