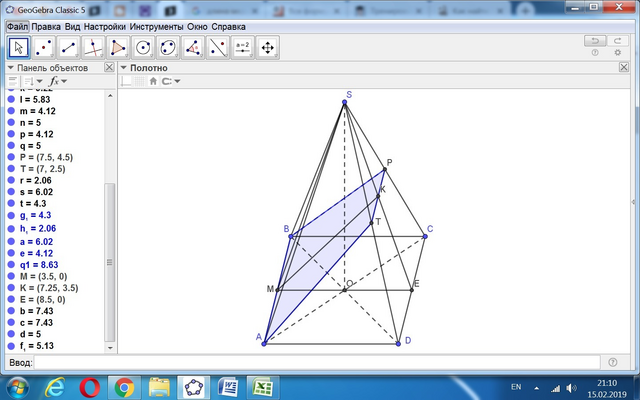
Пусть имеем пирамиду SABCD. В сечении трапеция АВРТ, где РТ - средняя линия грани CDS.
Находим апофему А боковой грани.
А = √(b² - (a/2)²) = (√(4b² - a²))/2.
Проведём осевое сечение через апофемы противоположных граней. В сечении равнобедренный треугольник MSE. Медиана MК в этом треугольнике - высота h искомого сечения.
Достроим треугольник до параллелограмма.
Согласно теореме, сумма квадратов диагоналей (A и 2h) параллелограмма равна удвоенной сумме квадратов его сторон (А и а): 2(А² + а²) = А² + (2h)².
4h² = 2A² + 2a² - A² = A² + 2a². Подставим вместо А её значение.
h² = ((b² - (a/2)²) + 2а²)/4 = (4b² + 7a²)/16.
h = √(4b² + 7a²)/4.
Площадь S искомого сечения равна:
S = ((a + (a/2))/2)*(√(4b² + 7a²)/4) = 3a√(4b² + 7a²)/16.