Пожалуйста, решите задачу определить математическое ожидание, дисперсию, вероятность...

Question

Дан 1 ответ

qwaaq_zn · Answer 1 · 2020-05-29T17:05:32+0000

Мат. ожидание определяется как

$M(X) = \sum X_{{i}}P \left( X_{{i}} \right) = -2\cdot 0.2+...+6*0.2=0.9$

Дисперсия есть

$D(X)=M(X^2)-[M(X)]^2=9.9-(0.9)^2=9.09$

(где $M(X^2) = \sum X_{{i}}^2P \left( X_{{i}} \right)$ )

Вероятность попадания в интервал (-1, 4] очевидно

$P(X \in (-1, 4])=0.2+0.1=0.3$ (что соотв. двум значения X: 0 и 4)

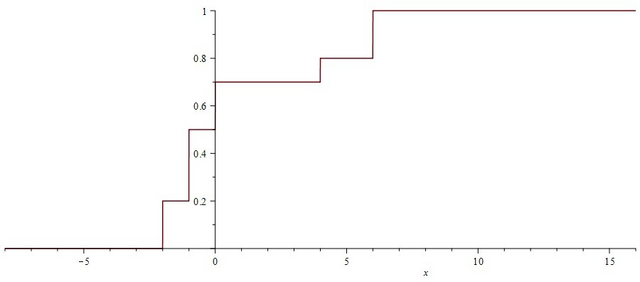
Функция распределения в прикрепленных файлах. Правда вертикальные линии соединяющие горизонтальные отрезки необходимо убрать, в этих точка функция терпит разрыв. И еще функция распределения непрерывна слева... Это значит что, например, в точке -1 у нижнего отрезка крайняя правая точка должна быть полностью закрашена, а у верхнего крайне левая обязана быть выколотой, как бы странно это не выглядело с логической точки зрения. Аналогично для других точек в которых есть разрыв.

Что есть полигон распределения я не знаю, но судя по примерам из интернета эта штука получится если убрать все линии из прикрепленного графика и оставить только точки соотв. значениям X и их вероятностям P.