Дано:
U0=32м/c
η=0,6
Найти:
Δt-?
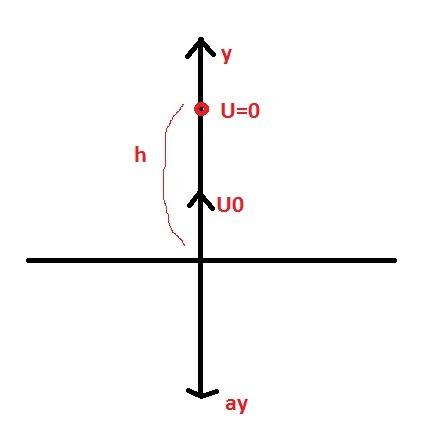
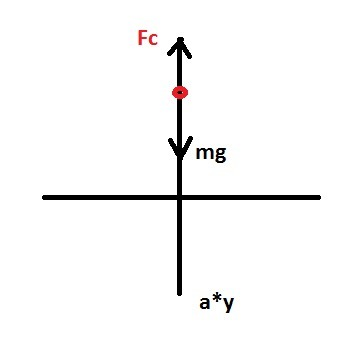
Вниз действуют сила mg+Fсопротивления/m=(1+η)mg\m=(1+η)g=ay

Теперь тело падает вниз:

Высота равна:

Подставим t1 которое нашли:

Вниз:
 t_2=\sqrt{\frac{2h}{ay^*} }=\sqrt{\frac{U_0^2}{(1+\eta)g^2(1-\eta)} }=\frac{U_0}{g-\sqrt{1-\eta^2} }" alt="h=\frac{ay^*t_2^2}{2}=>t_2=\sqrt{\frac{2h}{ay^*} }=\sqrt{\frac{U_0^2}{(1+\eta)g^2(1-\eta)} }=\frac{U_0}{g-\sqrt{1-\eta^2} }" align="absmiddle" class="latex-formula">
t_2=\sqrt{\frac{2h}{ay^*} }=\sqrt{\frac{U_0^2}{(1+\eta)g^2(1-\eta)} }=\frac{U_0}{g-\sqrt{1-\eta^2} }" alt="h=\frac{ay^*t_2^2}{2}=>t_2=\sqrt{\frac{2h}{ay^*} }=\sqrt{\frac{U_0^2}{(1+\eta)g^2(1-\eta)} }=\frac{U_0}{g-\sqrt{1-\eta^2} }" align="absmiddle" class="latex-formula">
Отсюда
Δt:

Подставив значения имеем:

Ответ: 6c