Решите треугольник ABC, если AB= корень из 3 см, AC=2 корня из 3 см, угол A=60 гр.

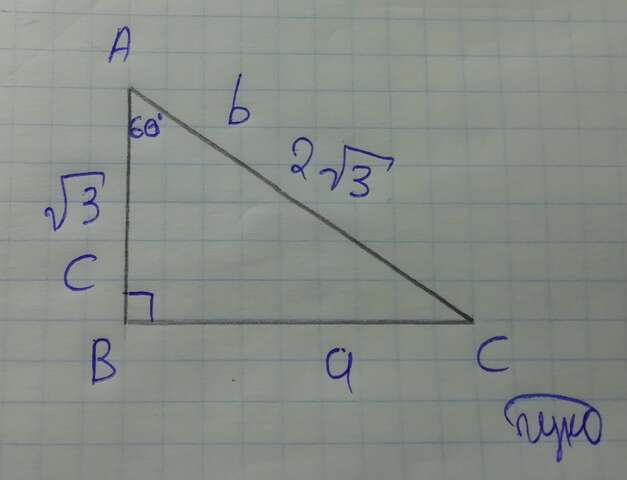
Используем теорему косинусов

a² = b² + c² - 2bc * cosA

Подставляем

a² = (2√3)² + (√3)² - 2 * 2√3 * √3 * cos60°

a² = 12 + 3 - 12 * 0,5

a² = 12 + 3 - 6

a² = 9

a = √9 = 3

По теореме синусов

$\displaystyle \frac{a}{sinA}=\frac{c}{sinC} \\\\\\\frac{3}{sin60} =\frac{\sqrt{3} }{sinC} \\\\\\sinC=\frac{\sqrt{3}\times \displaystyle\frac{\sqrt{3} }{2}}{3} \\\\\\sinC=\frac{3:2}{3} =\frac{1.5}{3} =0.5$

Синус в 0,5 есть угол в 30° ==> ∠C = 30°

∠B = 180 - 60 - 30 = 90°

Ответ: BC = 3 см, ∠C = 30°, ∠B = 90°