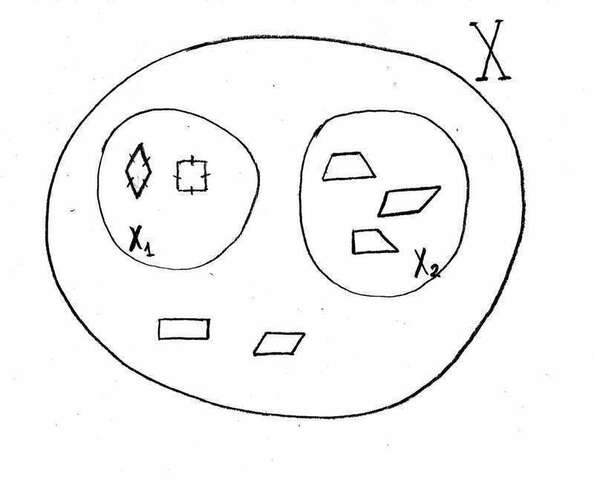
Множество Х разбито на классы Х1 и Х2, если:
1) подмножества Х1 и Х2 не пересекаются,
2) объединение подмножеств Х1 и Х2 совпадает с множеством Х.
Если не выполнено хотя бы одно из условий, классификацию считают неправильной.
1) Ромб - это четырехугольник, у которого все стороны равны между собой.
Трапеция - это четырехугольник, у которого две стороны параллельны, , а две другие - нет.
Подмножества Х1 и Х2 не пересекаются, т.к. ни один ромб не может быть трапецией, и ни одна трапеция не может быть ромбом.
2) Объединение подмножеств Х1 и Х2 не совпадает с множеством Х, т.к., объединив подмножества Х1 и Х2, мы получим множество ромбов и трапеций, а в него не будет входить множество параллелограммов (кроме одного частного случая - квадрата). Параллелограмм - это четырехугольник, который имеет две пары параллельных сторон.
Одно из условий не выполнено, значит, разбиение множества Х на классы Х1 и Х2 не произошло.