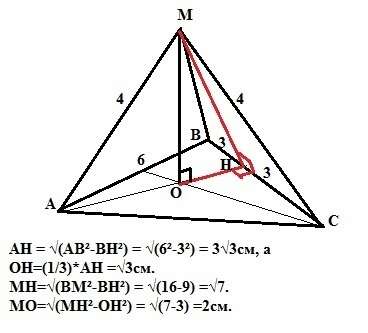
Соединим точку М с вершинами треугольника АВС. Получим правильную пирамиду (так как в основании лежит правильный треугольник, а боковые грани этой пирамиды равны ), вершина М которой проецируется в центр основания .
Проведем АН - высоту правильного треугольника АВС.
В правильном треугольнике АН - высота и медиана. Тогда
АН = √(АВ²-ВН²) = √(6²-3²) = 3√3см, а
ОН=(1/3)*АН =√3см (по свойству медианы, которая делится точкой О в отнршении 2:1, считая от вершины).
Соединим точку М с точкой Н.
МН перпендикулярна ВС по теореме о трех перпендикулярах.
Тогда из прямоугольного треугольника МВН с катетом ВН=3 и гипотенузой ВМ = 4 имеем катет МН=√(ВМ²-ВН²) = √(16-9) =√7.
Из прямоугольного треугольника МОН с катетом ОН=√3 и гипотенузой ВМ = √7 имеем катет МО=√(МН²-ОН²) = √(7-3) =2см.