1)

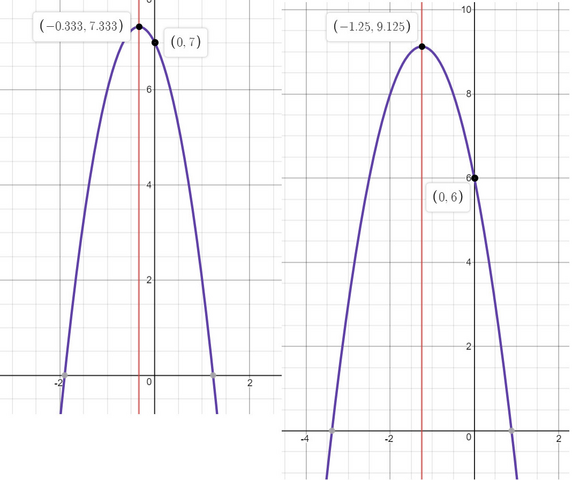
Это парабола, которая направлена вниз, координаты вершины (-1/3;7(1/3)), ось симметрии соответственно это x=-1/3, найдём точки пересечения с осями:

Есть всё чтобы построить.
2)

Это парабола ветви которой вниз, координаты вершины (1,25;9,125), ось симметрии x=-1,25. График пересекает оси в точка:

Строим.