Ответ:
Sabc = 12,5 ед².
Объяснение:
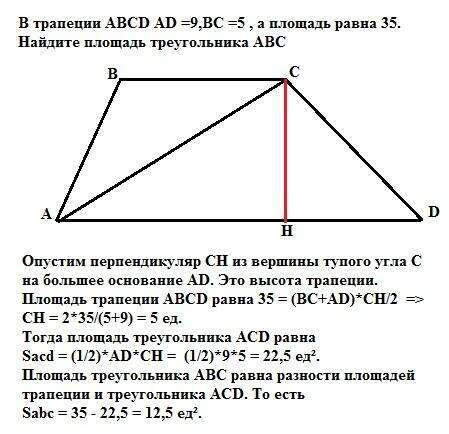
Опустим перпендикуляр СН из вершины тупого угла С на большее основание AD. Это высота трапеции.
Площадь трапеции АВСD равна 35 = (BC+AD)*CH/2 =>
СН = 2*35/(5+9) = 5 ед.
Тогда площадь треугольника ACD равна
Sacd = (1/2)*AD*CH = (1/2)*9*5 = 22,5 ед².
Площадь треугольника АВС равна разности площадей трапеции и треугольника ACD. То есть
Sabc = 35 - 22,5 = 12,5 ед².