1) Если не указана конкретная прямая, к которой касательная параллельна, то ответить можно в общем виде:
касательная параллельна любой прямой, угловой коэффициент которой равен производной функции в точке касания.
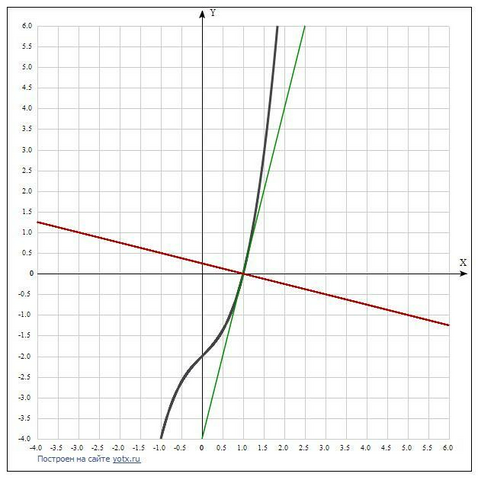
2) Дана функция y=x³+x-2. Производная равна y' = 3х² + 1.
Значение y'(1)=3*1² + 1 = 4.
Значение функции у(1) = 1³ + 1 - 2 = 0.
Уравнение касательной: у = 4(х - 1) + 0 = 4х - 4.
Уравнение нормали: у = (-1/4)(х - 1) + 0 = (-1/4)х + (1/4).