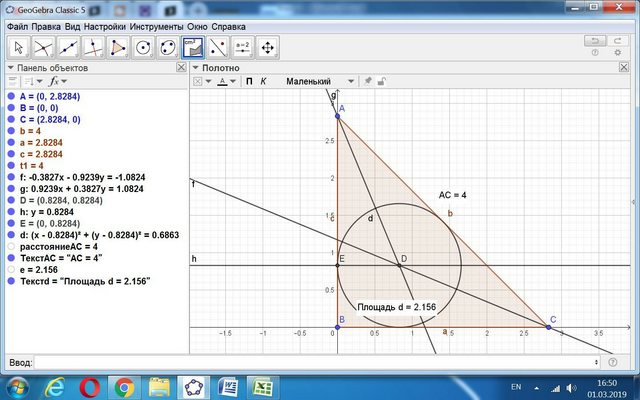
Катеты равны: 2х² = 4², х = √(16/2) = √8 = 2√2 см.
Площадь треугольника равна S = (1/2)*(2√2)² = 8/2 = 4.
Полупериметр р = (2*2√2 + 4)/2 = (2√2 + 2) см.
Радиус вписанного круга равен r = S/p = 4/(2√2 + 2) = 2/(√2 + 1).
Площадь его равна πr² = 4π/(√2 + 1)² ≈ 2,156 см².