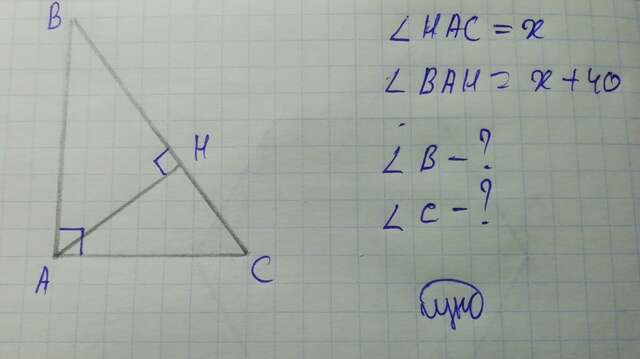
Пусть x - меньший угол из двух образующихся при пересечении высоты с прямым углом, тогда больший равен x + 40. Получим уравнение
x + x + 40 = 90 (прямой угол равен 90°)
2x + 40 = 90
2x = 90 - 40
2x = 50
x = 50/2 = 25° = ∠HAC
Больший угол равен x + 40 = 25 + 40 = 65° = ∠BAH
Рассмотрим ΔABH - прямоугольный: ∠A = 65°, ∠H = 90°, ∠B - ?
∠B = 90 - ∠A = 90 - 65 = 25° (сумма острых углов прямоугольного треугольника равна 90°)
∠C = 90 - 25 = 65° (сумма острых углов прямоугольного треугольника равна 90°)