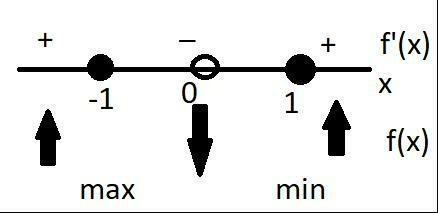
На координатной прямой х, отмечаем точки 1 и -1, получается что производная положительная (функция возрастает), когда x>1 и x<-1, а отрицательна (функция убывает), когда -1<x<1, в точках -1 и 1 производная равна нулю, а знак с минуса на плюс меняется в точке 1, значит точка минимума x=1</p>
Ответ: 1.