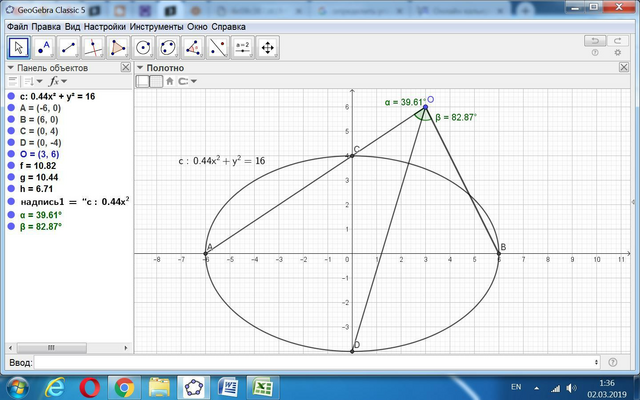
Преобразуем уравнение окружности с выделением полных квадратов.
Получаем (х - 3)² + (у - 6)² = 9.
Отсюда определяем координаты точки О - центра этой окружности.
О(3; 6).
Координаты концов осей эллипса берём прямо из заданного уравнения:
- большая ось А(-6; 0) и В(6; 0).
- малая ось С(4;0) и Д(-4; 0).
Определяем угол СОД (для малой оси).
Найдем вектор по координатам точек:
СО = {Оx - Сx; Оy - Сy} = {3 - (-6); 6 - 0} = {9; 6}
DО = {Dx - Оx; Dy - Оy} = {3 - 0; 6 - (-4)} = {3; 10}
Найдем скалярное произведение векторов:
СО · ОD = СОx · ОDx + СОy · ОDy = 9 · 3 + 6 · 10 = 27 + 60 = 87
Найдем длины векторов:
|СAО| = √(СОx² + СОy²) = √(9² + 6²) = √(81 + 36) = √117 = 3√13
|ОD| = √(ОDx² + ОDy²) = √(3² + 10²) = √(9 + 100) = √109
Найдем угол между векторами:
cos α = СО · ОD
|СО||ОD|
cos α = 87/(3√13 · √109
) ≈ 0,77039.
α = arc cos 0,77039 = 0,69134 радиан или 39,6107 градуса.
Для большей оси расчёт аналогичен.
Найдем вектор по координатам точек:
AB = {Bx - Ax; By - Ay} = {3 - (-6); 6 - 0} = {9; 6}
CD = {Dx - Cx; Dy - Cy} = {3 - 6; 6 - 0} = {-3; 6}
Найдем скалярное произведение векторов:
AB · CD = ABx · CDx + ABy · CDy = 9 · (-3) + 6 · 6 = -27 + 36 = 9
Найдем длины векторов:
|AB| = √ABx2 + ABy2 = √92 + 62 = √81 + 36 = √117 = 3√13
|CD| = √CDx2 + CDy2 = √(-3)2 + 62 = √9 + 36 = √45 = 3√5
Найдем угол между векторами:
cos α = AB · CD
|AB||CD|
cos β = 9/(3√13 · 3√5) ≈ 0,12403.
β = arc cos 0,12403 = 1,4464 радиан или 82,875 градуса.