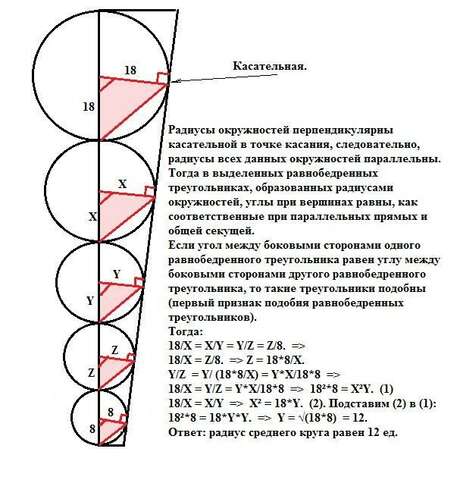
Радиусы окружностей перпендикулярны касательной в точке касания, следовательно, радиусы всех данных окружностей параллельны. Тогда в выделенных на рисунке равнобедренных треугольниках, образованных радиусами окружностей, углы при вершинах равны, как сответственные при параллельных прямых и общей секущей.
Если угол между боковыми сторонами одного равнобедренного треугольника равен углу между боковыми сторонами другого равнобедренного треугольника, то такие треугольники подобны (первый признак подобия равнобедренных треугольников).
Тогда:
18/X = X/Y = Y/Z = Z/8. =>
18/X = Z/8. => Z = 18*8/X.
Y/Z = Y/ (18*8/X) = Y*X/18*8 =>
18/X = Y/Z = Y*X/18*8 => 18²*8 = X²Y. (1)
18/X = X/Y => X² = 18*Y. (2). Подставим (2) в (1):
18²*8 = 18*Y*Y. => Y = √(18*8) = 12.
Ответ: радиус среднего круга равен 12 ед.