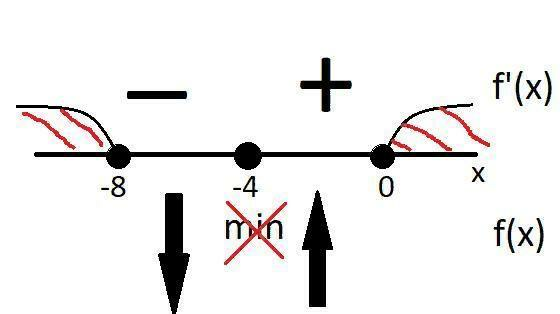
\left[\begin{array}{ccc}x\leq-8\\x\geq0\\\end{array}" alt="y=\sqrt{x^2+8x}\\y'=\frac{(x^2+8x)'}{2\sqrt{x^2+8x}}=\\\frac{2x*1+8}{2\sqrt{x^2+8x}}=\frac{x+4}{\sqrt{x^2+8x}};\\x^2+8x\geq0=>\left[\begin{array}{ccc}x\leq-8\\x\geq0\\\end{array}" align="absmiddle" class="latex-formula">
Когда производная положительная функция возрастает, когда отрицательная - убывает.
Ответ: убывает - (-∞;-8]
возрастает - [0;+∞)
