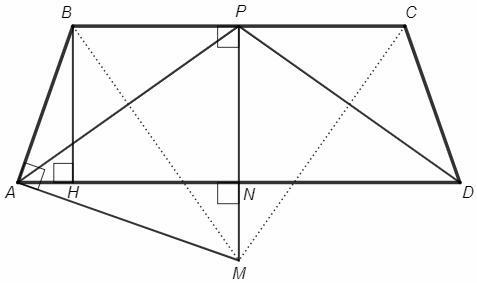
P - точка пересечения биссектрис. Биссектриса внутреннего угла при параллельных отсекает равнобедренный треугольник.
AB=BP=PC=CD=3, BC=6
Опустим высоту BH на AD.
AH=(AD-BC)/2 =(8-6)/2 =1
BH=√(AB^2-AH^2) =√(9-1) =2√2
Точка M равноудалена от прямых AB, BC, CD, следовательно лежит на биссектрисах углов ABC и BCD. Эти биссектрисы делят равные углы пополам и образуют равнобедренный треугольник. MP - серединный перпендикуляр к BC.
В равнобедренном треугольнике ABP биссектриса BM является серединным перпендикуляром к AP. AM=PM, △BAM=△BPM по трем сторонам, ∠BAM=∠BPM=90.
MP пересекает AD в точке N.
∠MAN=90-∠BAD=∠ABH, △MAN~△ABH
MN/AH=AN/BH => MN=4/2√2 =√2