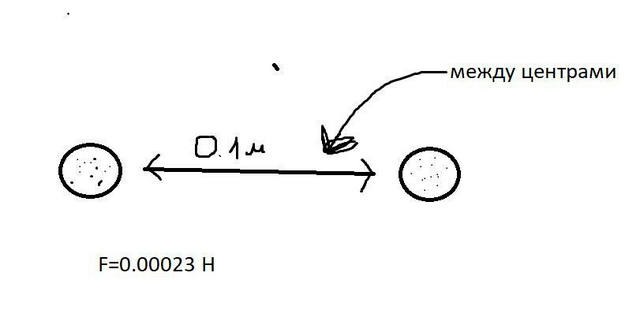
Сила взаимодействия заряженных тел, то есть сила Кулона:

Где 
q это заряды шариков
r расстояние между ними
Так как заряды одинаковые, то запишем:

Отсюда 
Но стоит понимать, что шарик имеет заряд именно из-за множества электронов сидящих на нём.
Каждый из них имеет элементарный заряд e, который равен  Пусть на каждом шарике их сидит N штук.
Пусть на каждом шарике их сидит N штук.
Тогда делаем вывод, что