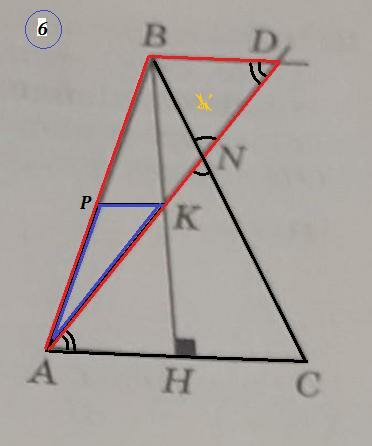
6) ΔАВС - равнобедренный , К - середина высоты ВН , ВД║АС .
Проведём КР║АС ⇒ ΔАКР подобен ΔАВД (по двум углам , ∠АВД=∠АРК , ∠АДВ=∠АКР ), причём т.к. К - середина ВН, то АР/АВ=1/2.
Из подобия ⇒ РК/ВД=АР/АС=1/2 ⇒ ВД=2*РК , РК=1/2*ВД .
РК - половина средней линии ΔАВН, а ср. линия Δ = половине стороны Δ, которой она параллельна, то есть ср. линия Δ=1/2*АН. Тогда РК=1/2*АН=1/2*1/2*АС=1/4*АС , 1/4*АС=1/2*ВД ⇒ АС=2*ВД .
ΔANC подобен ΔBNД (по двум углам: ∠ANC=∠BNД как вертик., ∠ВДN=∠NAC внутр. накрест лежащие) ⇒
BN/NC=ВД/АС=ВД/(2*ВД)=1/2
7) ΔАСВ , С=90° , СД⊥АВ , СД=6 , ВД=х , АД=х-5 ,
СД⊥АВ ⇒ СД²=АД*ВД ⇒ 6²=(х-5)*х , 36=х²-5х , х²-5х-36=0 , D=169=13² , x= -4<0 ( не подходит) , x=9 .</p>
АВ=АД+ВД=(9-5)+9=4+9=13
8) ΔАВС , ∠С=90° , СД⊥АВ , ДВ=3,2 , АД=1,8
СД⊥АВ ⇒ АС²=АД*АВ , АС²=1,8*(1,8+3,2)=1,8*5=9 ⇒ АС=3
9) ΔАВС , ФDFE - ромб ⇒ диагонали ромба перпендикулярны: DE⊥AF , DE=6 cм , AF=8 см ⇒ DO=3 см , FO=4 см ⇒ ΔDOF - прямоугольный египетский Δ ⇒ DF=5 cм ( или найти DF по теореме Пифагора) .
BF:FC=2:3 ⇒ BF:BC=2:(2+3)=2:5 .
Так как DF║АЕ ( как стороны ромба), то DF║АС ⇒ ΔАВС подобен ΔBDF ⇒ DF:AC=BF:BC=2:5 ⇒ AC=(3*DF)/2=(5*5)/2=25/2=12,5 см.