Область определения: x-2≠0 ⇒ x≠2
Преобразуем:

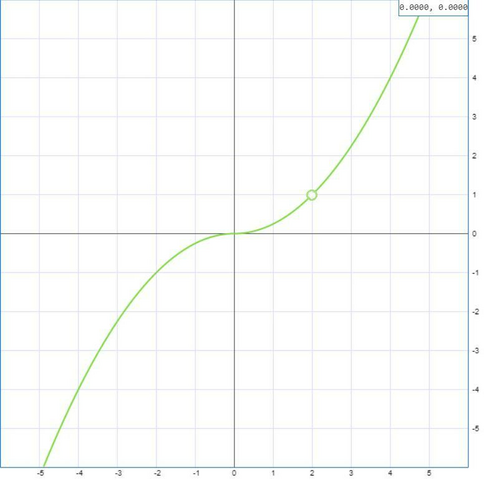
При положительных x графиком является кусок параболы с ветвями вверх, при отрицательных - кусок параболы с ветвями вниз. В итоге получается нечто напоминающее гиперболу.
Точки для построения: (-5; -6.25), (-4; -4), (-3; -2.25), (-2; -1), (-1; -0.25), (0; 0), (1; 0.25), (2; 1) - выколота, (3; 2.25), (4; 4), (5; 6.25)