Правильный треугольник - равносторонний(все стороны равны)
Если периметр известен, то найдем сторону: a=P/3=6√3/3=2√3(см)
Чтобы найти радиус описанной окружности, воспользуемся теоремой синусов:
a/siną = 2R => R=a/2siną = 2√3/2*sin60°= √3/√3/2=2(см)
Большая диагональ правильного шестиугольника равна удвоенному радиусу описанной = 2*2=4 (см)
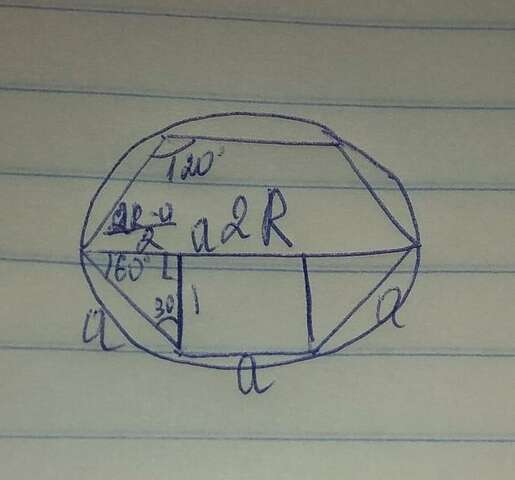
Рассмотрим трапецию , где сторона шестиугольника равна х.
Трапеция является равнобедренной, углы у основания равны по 60°(т.к. угол шестиугольника 120).Опустим из вершины меньшего основания высоту, получим прямоугольный треугольник, где есть угол 30 градусов. Далее из другой вершины проводки высоту, получаем прямоугольник . Кусочки большего основания равны(очевидно), и равны (2R-x)/2
По теореме угла 30 градусов в прямоугольном треугольнике выйдем в выражение: 2R-x = x, значит х = R
Периметр : 6*х= 6 * R = 6*2 = 12(см)
Ответ: 12 см.
P.S. на рисунке сторону обозначил не х, а а.