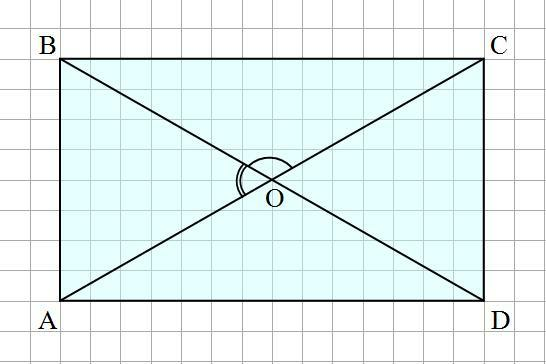
Дано: ∠ВОС = 120°; АС = 16 см.
Найти: АВ - ?
Решение: См. рис.
∠АОС - развернутый и равен 180°
Так как ∠АОС = ∠АОВ + ∠ВОС, то:
∠АОВ = ∠АОС - ∠ВОС = 180 - 120 = 60°
Диагонали прямоугольника делятся точкой пересечения пополам. Следовательно:
АО = ОВ = ОС = ОD
и ΔАОВ - равнобедренный с углом при вершине, равным 60° и равными углами при основании АВ.
Так как сумма внутренних углов треугольника равна 180°, то сумма углов при основании равна 120° и каждый угол равен 60°.
Таким образом, в ΔАОВ все углы равны, следовательно, данный треугольник равносторонний, с длиной стороны, равной половине диагонали:
АВ = АО = АС : 2 = 16 : 2 = 8 (см)
Ответ: 8 см.