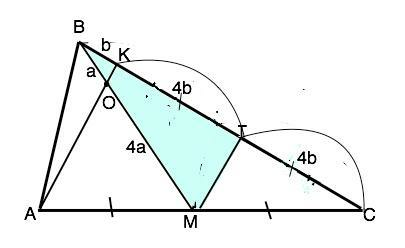
Прямая, проходящая через вершину А треугольника АВС и делящая медиану ВМ в отношении 1:4, считая от вершины, пересекает сторону ВС в точке К. Найдите отношение площадей треугольников ВОК и АВС, где О – точка пересечения АК и ВМ.
* * *
Проведем МТ║АК. Треугольники ВОК и ВМТ подобны по общему углу В и соответственным углам при пересечении их параллельных оснований секущими ( боковыми сторонами). ВК:КТ=ВО:ОМ=1:4. Для треугольника АКС отрезок МТ - средняя линия. Поэтому СТ=КТ=4 части, ⇒ ВС=ВК+КТ+ТС=9 частей.
Примем S(АВС)=1. Так как медиана треугольника делит его на два равновеликих, то Ѕ(ВМС)=1/2. Ѕ(ВМТ)=5/9 от Ѕ(ВМС). Ѕ(ВМТ)=(1/2):9•5==5/18 от площади АВС.
Треугольники МВТ и ОВК подобны. k=ВК:ВТ=1/5. Отношение площадей подобных треугольников равно квадрату коэффициента их подобия. ⇒ Ѕ (ВОК):Ѕ(ВМТ)=k²=1/25. Ѕ(ВОК)=5/18•1/25=1/90 от Ѕ(АВС). Отношение площадей треугольников ВОК и АВС равно 1:90