Отметьте на координатной плоскости точки M (6;6), N (-2;2), K (4;1) и P (-2;4). 1)...

Ось абсцисс - ось x.

Ось ординат - ось у.

Точка O(x;y) имеет координату x на оси х и координату у на оси у.

Можно просто аккуратно нарисовать и понять где пересекается, а можно вывести уравнение прямой (по двум точкам) и найт пересечение прямых.

$(x_1;y_1)+and+(x_2;y_2)\\(y_1-y_2)x+(x_2-x_1)y+(x_1y_2-x_2y_1)=0$

Таким образом создаётся уравнение прямой по двум точкам

1) $MN:(6-2)x+(-2-6)y+(12-(-12))=0\\4x-8y+24=0\\y=\frac{x}{2}+3\\KP:(1-4)x+(-2-4)y+(16-(-2))=0\\-3x-6y+18=0\\y=-\frac{x}{2} +3$

Найдём точку пересечения прямых по оси х, а потом подставим и найдём по оси у.

$-\frac{x}{2}+3=\frac{x}{2}+3\\x=0\\y=\frac{0}{2}+3=3$

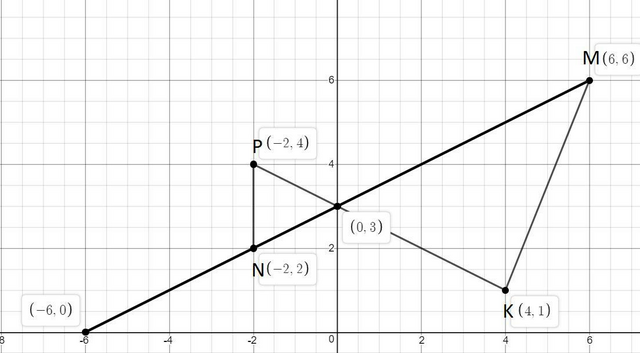
Ответ: (0;3)

2) Когда точка принадлежит оси х, то координаты по оси у, равны 0.

$y=\frac{x}{2}+3=0\\x=-6$

Ответ: (-6;0)

3) А когда точка принадлежит оси у, то координаты по оси х, равны 0.

$y=-\frac{x}{2}+3\\y=-\frac{0}{2}+3=3$

Ответ: (0;3)

Отметьте ** координатной плоскости точки M (6;6), N (-2;2), K (4;1) и P (-2;4). 1)...