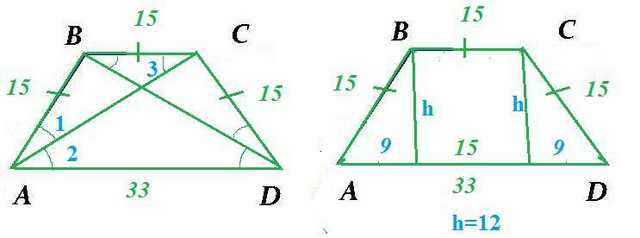
S=(a+b)·h/2
a=33
b=15
осталось найти h.
Так как диагонали являются биссектрисами острых углов, то
∠1=∠2
∠2=∠3 - внутренние накрест лежащие углы
Δ АВС - равнобедренный
АВ=ВС=СD=15 cм
Проводим высоты из вершин верхнего основания на нижнее.
Они разбивают трапецию на два равных прямоугольных треугольника
и прямоугольник.
В прямоугольных треугольниках гипотенуза 15, а катет
(33-15)/2=9
Тогда второй катет, являющийся высотой трапеции по теореме Пифагора равен 12.
h= 12=√(15²-9²)
О т в е т. S=(a+b)·h/2=(15+33)·12/2=288 см²