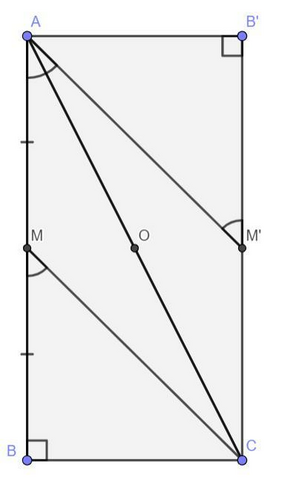
Достроим ΔABC до прямоугольника AB'CB. O - центр AC, эта точка является центром симметрии для прямоугольника. Поэтому, если M' - середина B'C, то CM║AM'.
∠BMC = ∠BAM', как соответственные углы при CM║AM' и секущей BA.
∠BAM' = ∠CAB+∠CAM' ⇒ ∠BAM'=∠BMC > ∠CAB. Первая часть неравенства доказана.
В прямоугольном ΔMBC (∠B=90°): MB
BM=AM т.к. CM - медиана.
В ΔMAC:
AM
Получили: ∠CAB > ∠ACM. Вторая часть неравенства доказана.
В итоге ∠BMC > ∠CAB > ∠ACM ч.т.д.