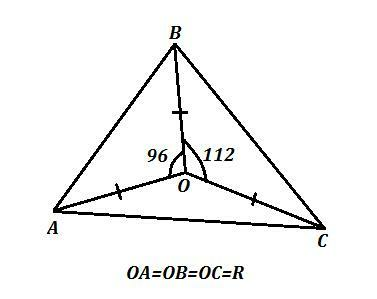
ΔАВС , R - радиус описанной окружности, точка О - её центр.
∠АОВ=96° , ∠ВОС=112° , ∠АОС=152°
Рассм. АОВ: АО=ВО=R ⇒ равнобедренный ⇒ углы при основании равны: ∠ОАВ=∠ОВА=(180°-96°)/2=42°
Аналогично, ΔВОС и ΔАОС - равнобедренные и
∠ОВС=∠ОСВ=(180°-112°)/2=34° ,
∠ОАС=∠ОСА=(180°-152°)/2=14° .
∠А=∠ОАВ+∠ОАС=42°+14°=56°
∠В=∠ОВА+∠ОВС=42°+34°=76°
∠С=∠ОСВ+∠ОСА=34°+14°=48°