Даю 100 баллов , т.к. самой нереально справиться) Помогите и мне ✨ Построить сечение...

Question

Даю 100 баллов , т.к. самой нереально справиться) Помогите и мне ✨ Построить сечение шестиугольной наклонной призмы по следу, проходящее через точку на ребре призмы и точку на верхнем основании параллельно следу. Распишите построение , не могу понять . Заранее благодарю !!! Обещаю , заставлю свой гуманитарный склад ума во всём разобраться )))

Comments

Есть рисунок? Прикрепите с помощью знака "скрепка"

---

Рисунка нет , нужно самим построить

---

Все равно, нельзя просто так выбрать точки, должны быть какие-то указания.

---

Любая точка на ребре и точка на верхнем основании параллельно следу . Всё есть только пример , на пятиугольный призме

---

Я думаю, что Вам дали две разные задачи. Построить сечение через точку на ребре параллельно следу и точку на верхнем основании параллельно следу.

---

По крайней мере разберетесь, что такое метод следов.

Answer 1

Следом называют прямую пересечения плоскости сечения и плоскости какой-либо грани многогранника.

Если понимать условие задания, что след "а" ДАН и сечение проходит через точку М на верхнем основании призмы ПАРАЛЛЕЛЬНО СЛЕДУ, то мы уже имеем прямую PQ, по которой плоскость сечения пересекает верхнее основание.

Точки Р и N принадлежат плоскости грани АА1В1В => имеем линию пересечения PN.

Точка Q принадлежит и плоскости сечения и плоскости EE1D1D. Продлив прямую DE до пересечения со следом в точке R и соединив точки Q и R прямой, получим точку G на ребре ЕЕ1 и линию пересечения QG. Продлив прямую EF до пересечения со следом в точке S и соединив точки G и S прямой, получим точку K на ребре FF1 и линию пересечения GK.

Соединив точки К и N, получим искомое сечение NPQGK.

---

Answer 2

Решение задачи во многом зависит от выбора точек.

Поэтому либо нужен  рисунок, на котором расположены точки, либо надо рассмотреть разные случаи.

Итак,

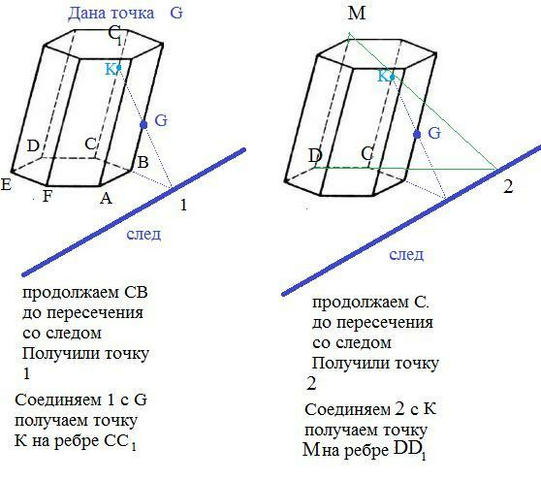
Если точка G на ребре ВВ₁  ближе к нижнему основанию cм. рис., то легко построить точку К на ребре СС₁.

Так как  проекцией точки G является точка В, а проекцией искомой точки К - точка С, то

соедив проекции, т.е В с С и продолжив до пересечения со следом, получим точку 1.

Соединяем точку 1 с точкой G  получаем точку К.

И так далее.

Главное:

прямые, содержащие точки секущей плоскости и прямые содержащие их проекции пересекаются на прямой, называемой СЛЕДОМ.

Через точку,  лежащую на верхнем основании,  проводим прямую, параллельную следу.

Получим 2  точки на сторонах верхнего основания.

Эта точка должна быть так выбрана, чтобы не было противоречия с положением точки К

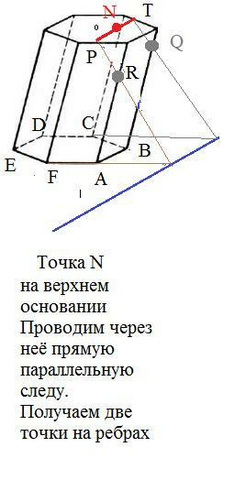
См. рис. точка N  на верхнем основании.

Проводим через точку N прямую, параллельную следу.

Эта прямая пересекает верхнее основание в точках P  и Т.

Проекция точки Р лежит на ЕА.

Продолжаем ЕА до пересечения со следом, получаем точку на следе. Соединяем эту точку с точкой Р и получаем точку на ребре АА₁

Аналогчно получим точку на ребре СС₁

Сечение

PTQR- параллельно следу, проходит через точку N на верхнем основании, но  не проходит через точку G, на ребре ВВ₁, выбранную в первом случае.

---

---