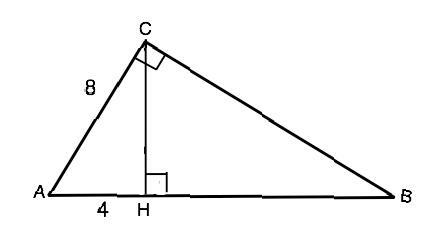
Отрезки гипотенузы, на которые делит её высота, являются проекциями катетов. АН - проекция АС на АВ.
Способ 1). Обратим внимание на то, что в треугольнике АСН катет АН равен половине гипотенузы АС. Значит, ∠АСН=30° (свойство), Из суммы углов треугольника ∠САН=180°-90°-30°=60°, ⇒ ∠АВС=30°. АС противолежит углу 30° ⇒ гипотенуза АВ=2•АС=16 см.
Способ 2). Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на треугольники, подобные друг другу и исходному треугольнику ( т.к. в каждом из них имеется равный острый угол). Из подобия следует АС:АВ=АН:АС, откуда АС²=АВ•АН. 64=АВ•4. ⇒ АВ=64:4=16 см.
Отсюда следует свойство, которое полезно помнить: каждый из катетов есть среднее пропорциональное между всей гипотенузой и его проекцией на гипотенузу.: АС²=АВ•АН