Постройте график функции

Question

Дан 1 ответ

Правильный ответ

$y=\begin{Bmatrix}x^2+4x+4,x\ge -4\\\frac{-16}{x},x<-4\end{matrix}$

Первая функция это парабола, разберёмся что у неё есть.

$y=x^2+4x+4=(x+2)^2$

Как оказалось это свелось к полному квадрату.

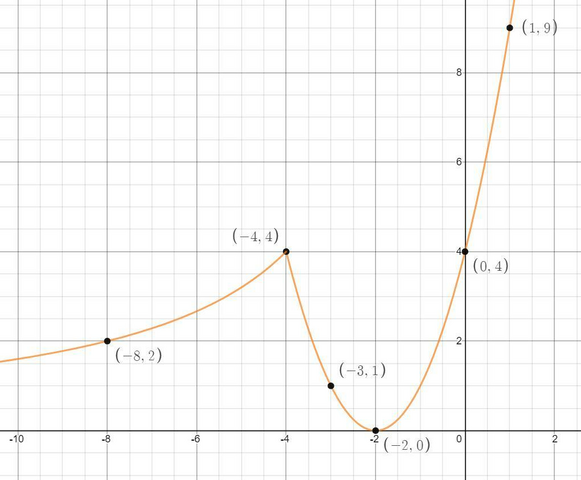
Получается, что у параболы ветви направлены вверх, координата вершины (-2;0), пересечение с осями координат: (0;4),(-2;0)

Найдём ординату точки границы определения этой функции и ещё пару точек для построения.

$y(-4)=(-4)^2+4\cdot (-4)+4=16-16+4=4,(-4;4)\\y(1)=1^2+4\cdot 1+4=1+4+4=9,(1;9)\\y(-3)=(-3)^2_4\cdot (-3)+4=9-12+4=1,(-3;1)$

Вторая функция это гипербола у которой асимптоты x=0 y=0, она лежит во 2 и 4 четверти относительно своих координат и не пересекает оси координат т.к. они же являются её асимптотами, найдём ординату границы области определения этой функции и ещё несколько точек, т.к. x< -4, то гипербола будет только во 2 четверти и меньше точек искать).

$y=\frac{-16}{x}\\y(-4)=\frac{-16}{-4}=4\\y(-8)=\frac{-16}{-8}=2$

Кстати точка (-4;4) особенная, в ней гипербола равноудалена от своих асимптот. В общем мы нашли всё для построения, границ функции сходятся, знак функция непрерывная, смотри график внизу.

WhatYouNeed_zn (34.7k баллов) 31 Май, 20